无题

无问夕故2024-09-102024-09-10

一、AE 自编码器

自编码器模型结构图

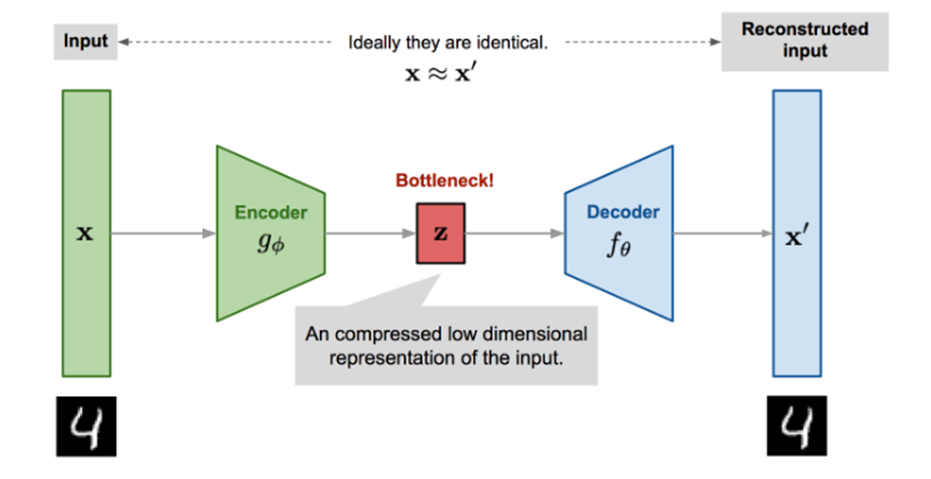
编码器网络可以将原始高维网络转换为潜在的低维代码

解码器网络可以从低维代码中恢复原始数据，并且可能具有越来越大的输出层

自编码器针对从代码重建数据进行了显式优化。一个好的中间表示不仅可以捕获潜在变量，而且有利于完整的解压缩过程。

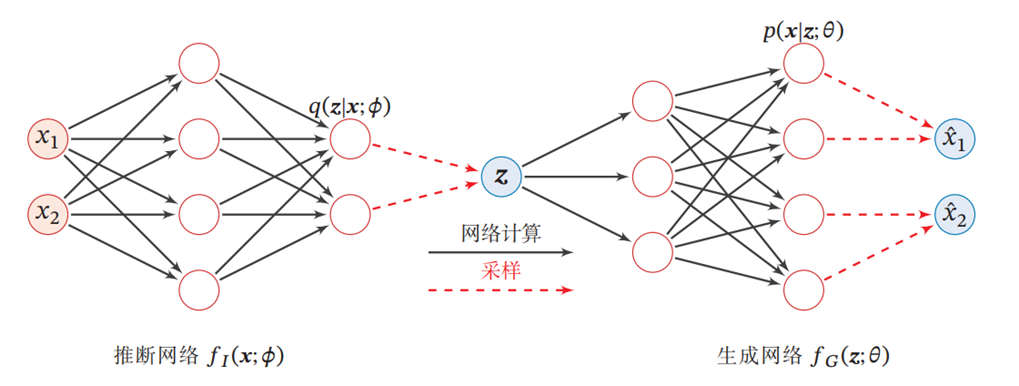
变分编码器和自动编码器的区别就在于：传统自动编码器的隐变量$z$的分布是不知道的，因此我们无法采样得到新的$z$，也就无法通过解码器得到新的$x$。

AE的缺点：映射空间不连续，无规则，无界

VAE将每组数据编码为一个分布

二、AEs 正则自编码器

去噪自编码器

在输入数据时加入噪声，强化特征提取能力

稀疏自编码器

dropout

对抗式自编码器

与GAN网络结合

三、VAE 变分自编码器

变分自编码器模型结构图

1. 数学知识

1.1 贝叶斯公式（Bayes Rule）

公式表述为：
$$
p(z|x) = \frac{p(x,z)}{p(x)} = \frac{p(x|z)p(z)}{p(x)} \tag{1}
$$

1.2 KL散度

$K-L$ 散度又被称为相对熵（relative entropy），是对两个概率分布间差异的非对称性度量。

假设$p(x)$ ，$q(x)$是随机变量上的两个概率分布，

在离散随机变量的情况下，相对熵的定义为：
$$
KL((p(x)||q(x))) = \sum p(x) \log{\frac{p(x)}{q(x)}} \tag{2}
$$
在连续随机变量的情况下，相对熵的定义为：
$$
KL((p(x)||q(x))) = \int p(x) \log{\frac{p(x)}{q(x)}}dx \tag{3}
$$

1.3 EM算法

EM算法(期望最大算法)是一种迭代算法，用于含有隐变量的概率参数模型的最大似然估计或极大后验概率估计。具体思想如下：
EM算法的核心思想非常简单，分为两步：Expection-Step和Maximization-Step

E-Step主要通过观察数据和现有模型来估计参数，然后用这个估计的参数值来计算似然函数的期望值

M-Step是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代之后似然函数都会增加，所以函数最终会收敛。

公式表述为：
$$
\ln{p_{\theta}(x)} = KL(q(z)||p_{\theta}(z|x)) + \int q(z) \ln{\frac{p_{\theta}(x,z)}{q(z)}}dz \tag{4}
$$

$$
= KL(q(z)||p_{\theta}(z|x)) + L_{\theta}(q,x)
$$

E-step:用来固定$\theta$，求 $q(z)$:
$$
q_{t+1}(z) = \mathop {argmax}{q}L{\theta_{t}}(q,x) \tag{5}
$$

如果$p_{\theta}(z|x))$ 可以得出，则 $q(z)$ 就等于$p_{\theta}(z|x))$ ，如果不能得出，就利用变分推断近似估计 $q(z)$

M-step:用来固定 $q(z)$ ，求 $\theta$:

$$
\theta_{t+1} = \mathop {argmax}{\theta}L{\theta}(q_{t+1},x) \tag{6}
$$

变分推断

参数估计：根据样本中提供的相关信息，对总体分布中的未知参数$z$进行估值

使用贝叶斯估计对未知参数估值：
$$
p(z|x) = \frac{p(x,z)}{p(x)} = \frac{p(x|z)p(z)}{p(x)} \tag{上述公式1}
$$
其中， $p(x|z)$ 为极大似然估计， $p(z)$ 为最大后验估计。然而贝叶斯估计中的分母 $p(x)$ 一般得不出结果，只能找一个与之相似的函数 $q(z) \approx p(z|x) $ 代替，并通过$K-L$散度求出函数间的近似程度。

目标函数：
$$
\min KL((q(z)||p(z|x))) \tag{2}
$$
则：

$$
KL((q(z)||p(z|x))) = \int q(z) \log{\frac{q(z)}{p(z|x)}}dz \tag{3}
=\int q(z) \log{\frac{q(z)}{p(x,z)}}dz + \ln{p(x)}
$$

$$
\ln{p(x)} = KL((q(z)||p(z|x))) + \int q(z) \log{\frac{p(x,z)}{q(z)}}dz \tag{4} = KL((q(z)||p(z|x))) + L(q)
$$

因为 $\ln{p(x)}$是与$z$无关的常量，并不改变，所以要求的目标函数$\min KL((q(z)||p(z|x)))$ 相当于$\max L(q)$ ，而变分贝叶斯学习可以通过 $q(z)$ 的迭代实现 $L(q)$ 的最大化，即$ELBO$变分下界，则：
$$
\max L(q) = \int q(z) \log{p(x,z)}dz - \int q(z) \log{q(z)}dz \tag{5}
$$
平均场理论：变分分布$q(z)$可以因式分解为$M$个互不相交的部分
$$
q(z) = \prod_{i=I}^{M}{q_i} \tag{6}
$$
则：

$$
ELBO = \max L(q) = \int q(z) \log{\frac{p(x,z)}{q(z)}}dz \tag{7}
$$

$$
= \int_z \prod_{i=1}^{M}{q_i}[ \log{p(x,z)} - \log{\prod_{k=1}^{M}q_{k}}]dz
$$

$$
= \int_z q_j [\prod_{i \neq j}^{M}{q_i} \log{p(x,z)}]dz - \int_{z}\prod_{i=0}^{M}q_{i}\sum_{k=1}^{M}\log{q_k}dz
$$
分别对➖左右进行计算
$$
Left = \int_z q_j [\prod_{i \neq j}^{M}{q_i} \log{p(x,z)}]dz \tag{8}
$$

$$
= \int_{z_j}q_j[\int_{z_{i \neq j}} \prod_{i \neq j}q_i\log{p(x,z)}dz_{i \neq j}]dz_j
$$

$$
= \int_{z_j} q_j \mathbb{E}_{i \neq j}[\log{p(x,z)}]dz_j
$$

$$
Right = \int_{z}\prod_{i=0}^{M}q_{i}\sum_{k=1}^{M}\log{q_k}dz + C1 \tag{9}
$$

$$
= \int_{z_j} q_j\log{q_j}dz_j \prod_{i \neq j}\int_{z_i}q_i dz_i + C1
$$

$$
= \int_{z_j} q_j\log{q_j}dz_j + C1
$$

其中：$C1 = - \int_z \prod_{i=0}^{M}q_i\sum{i \neq j}\log{q_j}dz$

同时，令$\log{\tilde{p}(x,z_j)} = \mathbb{E}_{i \neq j}[\log{p(x,z)}]+C2$ ($C2$用于归一化，等式左边对一个概率取对数，因此需要保证概率的性质)

则$ELBO$最终化为：
$$
ELBO = \int_{z_j} q_j \mathbb{E}{i \neq j}[\log{p(x,z)}]dz_j - \int{z_j} q_j\log{q_j}dz_j - C1 \tag{10}
$$

$$
= \int_{z_j} q_j\log{\frac{\tilde{p}(x,z_j)}{q_j}}dz_j + C3
$$

$$
= - KL(q_j||\tilde{p}(x,z_j)) + C3
$$

则当$q_j \rightarrow \tilde{p}(x,z_j)$时，$ELBO$最大，即$L(q)$取最大值
$$
\log{q_j(z_j)} = \log{\tilde{p}(x,z_j)} \tag{11}
$$

$$
= \mathbb{E}_{i \neq j}[\log{p(x,z)}]+C2
$$

则：
$$
q_j(z_j) = \exp{( \mathbb{E}_{i \neq j}[\log{p(x,z)}]+C2)} \tag{12}
$$

$$
\int_{z_j}q_j(z_j)dz_j = \exp{(C2)}\int_{z_j}\exp{(\mathbb{E}_{i \neq j}[\log{p(x,z)}])}dz_j
$$

可以求出：
$$
C2 = \log{\frac{1}{\int_{z_j}\exp{(\mathbb{E}{i \neq j}[\log{p(x,z)}])}dz_j}} \tag{13}
$$
返回带入公式12，得出：
$$
q_j(z_j) = \frac{\exp{( \mathbb{E}{i \neq j}[\log{p(x,z)}])}}{\int_{z_j}\exp{(\mathbb{E}_{i \neq j}[\log{p(x,z)}])}dz_j} \tag{14}
$$

公式推导

参数	含义	数学表示	含义
$x$	观测数据	$q_{\phi}(z	x)/q_{\phi}z$
$z$	隐变量	$p_{\theta}(z	x)$
$\phi$	变分参数(近似后验分布的参数)	$p_{\theta}(x,z)$	生成数据 $x$ 和隐变量 $z$ 的联合概率分布
$\theta$	生成模型的参数	$p_{\theta}(x	z)$

在变分自编码器（VAE）的推导过程中，我们使用变分推断来近似真实后验分布，并且通过优化目标函数来学习生成模型的参数。

推导过程

目标：最大化数据的对数似然

变分自编码器的目标是最大化观测数据 $x$ 的对数似然，即：
$$
\log p_{\theta}(x) \tag{1}
$$
由于计算 $p_{\theta}(x)$ 直接计算非常困难，我们通过引入隐变量 $z$ 和变分推断来简化。
引入隐变量

根据隐变量的定义，我们可以将对数似然分解为：
$$
\log p_{\theta}(x) = \log \int_{z} p_{\theta}(x, z) , dz \tag{2}
$$
应用变分下界（ELBO）

为了优化这个目标，我们引入变分分布 $q_{\phi}(z|x)$ 来近似真实后验分布 $p_{\theta}(z|x)$。通过引入变分分布，我们可以使用变分下界（Evidence Lower Bound, ELBO）来逼近对数似然。ELBO 的推导如下：
$$
\log p_{\theta}(x) = \log \int_{z} p_{\theta}(x, z)dz \tag{3}
$$
引入变分分布 $q_{\phi}(z|x)$：
$$
\log p_{\theta}(x) = \log \int_{z} \frac{q_{\phi}(z|x)}{q_{\phi}(z|x)} p_{\theta}(x, z) , dz \tag{4}
$$

使用对数的变换性质：
$$
\log p_{\theta}(x) = \log \left[ \int_{z} q_{\phi}(z|x) \frac{p_{\theta}(x, z)}{q_{\phi}(z|x)} , dz \right]
$$

应用对数-期望的变换：
$$
\log p_{\theta}(x) \geq \mathbb{E}{q{\phi}(z|x)} \left[ \log p_{\theta}(x, z) - \log q_{\phi}(z|x) \right] \tag{5}
$$

这个期望值被称为变分下界（ELBO）：
$$
\text{ELBO} = \mathbb{E}{q{\phi}(z|x)} \left[ \log p_{\theta}(x, z) - \log q_{\phi}(z|x) \right] \tag{6}
$$
其中：
$$
\text{ELBO} = \mathbb{E}{q{\phi}(z|x)} \left[ \log p_{\theta}(x|z) \right] - \text{KL}(q_{\phi}(z|x) , || , p_{\theta}(z)) \tag{7}
$$
这里，KL 散度（Kullback-Leibler divergence）是：
$$
\text{KL}(q_{\phi}(z|x) , || , p_{\theta}(z)) = \int_{z} q_{\phi}(z|x) \log \frac{q_{\phi}(z|x)}{p_{\theta}(z)} , dz \tag{8}
$$
优化目标

最终的目标是最大化 ELBO，从而间接最大化对数似然。通过优化变分参数 $\phi$ 和生成参数 $\theta$，使得 ELBO 最大化，即可获得最优的模型参数。
总结
- 近似后验 $ q_{\phi}(z|x) $：通过变分推断来近似真实后验。
- 真实后验 $ p_{\theta}(z|x) $：目标是通过优化得到近似。
- 生成模型 $ p_{\theta}(x, z) $：模型定义生成数据的过程。
- 条件概率分布 $ p_{\theta}(x|z) $：表示给定隐变量 $z$ 的情况下数据 $x$ 的分布。

VAE 的关键在于利用 ELBO 来进行模型优化，通过最大化 ELBO 来逼近真实对数似然，从而获得高效的生成模型。